DIY Freeze Dryer

From Makers Local 256
Jump to: navigation, search

Creator:
Candleknight
Status:
Research, Design, and materials acquisition
Born On:
11:51, 22 February 2012 (CST)
Last Updated:
13:30, 02 September 2014 (CDT)

Overview

This is a project to try and build a reasonably priced, reasonably functional, freeze drying machine at home.

  • UPDATE(05/12/14): Hey look! An update! XD I got a bit burned out and ADHD-ed away from this project for a while to work on other stuff. I really feel like finishing this now and actually taking it somewhere, so I'm getting back into it now and resuming work. More info and progress should be forthcoming soon!

Purpose

Commercially available freeze drying units, even relatively small ones, are really expensive. We're talking in the thousands of dollars. This got me to thinking. In theory at least, the physics behind freeze drying and how it works aren't terribly complicated, so I figure I'll give a crack at making a decent one from scratch and save myself a few thousand bucks, and if it works other people on the internet will be able to follow my instructions and build one for themselves as well.

Info

Phase Diagram of Water

Progress

Acquire Vacuum Pump

  • Found a vacuum pump on sale at harbor freight for $110. It pumps 3cfm and is rated to pull a vacuum down to 3 Pascal. I believe it is supposed to be used to pull a vacuum to clean out AC systems and refrigeration coils.

Vacuum Pump Harbor Freight 3CFM.jpg


Vacuum Pump and Connector System Prototype

  • The vacuum pump I got has 2 input ports: 1/4" SAE & 1/2" Acme. Finding stuff to fit these decently was a giant pain in the rear, but I've finally managed to get a setup that is tightly sealed, readily available, and not too expensive.
    • Go to the plumping section in Lowes (or where ever) and get 1/4" polyethylene tubing. It's milky white, the same size as fish tank tubing, and about $2 for a 25' coil. You'll also want to get the 1/4" brass compression connectors that fit it. I've found that with good use of teflon thread tape the 1/4" female connector will fit pretty well on the 1/2" Acme connector of the vacuum pump. Don't ask me why, the people that categorize hardware just pick whatever measurements they feel like using to describe stuff, it seems. Probably the same people that decided that 2x4 planks would be 1.5"x3.5".
    • Anyways, at minimum you're going to need these connectors:
      • 1x 1/4" FIP to compression
      • 2x T-shaped compression-compression valve
      • 1x T-shaped 3 way compression coupling
    • Use thread tape and screw the female adapter onto the vacuum pump.
    • Then use tubing to connect that to the first T valve
      • This first valve is your main flow control valve. You need it so you can seal off the system after you've pulled a vacuum. If you don't have it, then once you turn the vacuum pump off the vacuum in the chamber starts pulling air backwards through the pump. This degrades your vacuum pretty quickly, but even worse it can pull oil from the compressor trough the lines and contaminate your entire system. I found that one out the hard way. It is not fun.
      • Your order of operations should be:
        1. Turn on pump
        2. Open Valve
        3. Pull vacuum
        4. Close valve
        5. Turn off pump
    • Connect that to the T splitter
    • One end of the T splitter should connect to the second T Valve
      • This second valve is your release valve and just connects to the open air. You need it to let air back into the vacuum chamber once you're done. Otherwise you have to try and pry the lid off, and 14.7 psi makes that really difficult in most cases.
    • The other connection on the T splitter is the main line that runs to the vacuum chamber

Vacuum Chamber Prototype, Proof of Concept


V2 Vacuum Pump and Connector System Prototype

  • Alright, now it's time to take things up a notch. This version will have a much larger vacuum chamber volume, as well as a more robust, well sealed connector system.
  • I've heard through various channels that when pulling a high vacuum you actually (somewhat counter-intuitively) need a bigger diameter tubing than with normal pressures in order to maintain a decent flow rate. The reason is the way that the gas molecules behave in a low pressure environment. Lower pressure in this case also means fewer molecules per unit of volume, meaning there are fewer molecules behind each one to push it forward. And some stuff... ...more explanation...

Next Steps

Vacuum Chamber Construction

Door

It may be overkill, but I'm thinking of using a 1/2" sheet of Polycarbonate (Lexan) from eStreetPlastics for the door. With more careful analysis and design I could probably use a thinner sheet, but I've never built a vacuum chamber before so I'm overdesigning the crap out of this one. Also, you could skip this material altogether and just use the side of the pressure vessel that you cut off as the door, but I want to be able to see into the chamber.
I chose polycarbonate (Lexan) over acrylic (Plexiglass) because the polycarbonate is much stronger, more resilient, and has a higher working temperature.
Polycarbonate:

  • Melting temperature (Tm) 267 °C*
  • Glass transition temperature(Tg) 150 °C
  • Upper working temperature 115–130 °C
  • Lower working temperature −40 °C


  • Young's modulus (E) 2.0–2.4 GPa
  • Tensile strength (σt) 55–75 MPa
  • Compressive strength (σc) >80 MPa
  • Elongation (ε) @ break 80–150%
  • Poisson's ratio (ν) 0.37


Chamber Body

After some consideration, I'm thinking of using some sort of pre-constructed pressure vessel as the body of the vacuum chamber. Something like a propane tank, or a compressed air tank. My reasoning is that, at least for medium scale, if something is designed to hold 140 psi positive pressure, then it should maybe probably be able to hold 14.7 psi negative pressure. Yeah yeah yeah, I know that the structural design for the two things is not exactly the same, but I'm building in a factor of safety of nearly 10x, so I'm modestly confident that this won't implode.
I'm thinking that an old 10 to 20 gallon auxiliary compressed air tank will be a good place to start with this design. My plan is to use a torch, plasma cutter, or angle grinder cutoff wheel to cut off one end(one of the rounded ends). That will leave a round, flat opening on that end. I'll then weld on some sort of flange, add some sort of o-ring / seal, and then the Lexan door should just sit flush against it.


Vapor Deposition Cryo-coils/Condenser Plates?

Still looking into this to see if it's really necessary

  • UPDATE(2/28/12): After playing with the prototype mason jar vacuum chamber I have concluded that this element will, in fact, be necessary. Even doing small slices of apple, the water vapor destroys the vacuum completely in less than 10 minutes. So unless I want to run the vacuum pump continuously, I'm going to have to put in Vapor Deposition Cryocoils.
    • I need to do some more research on this subject, but initially I'm thinking that pulling the coils out of a mini fridge, portable/mini freezer, window A/C unit, or something like that might do the job.
      • May have to consult with a HVAC professional about cutting & reattaching the lines, since I'll need some way to get them through the wall of the vacuum chamber.
      • Might could just make notches at the seal to do this more easily.


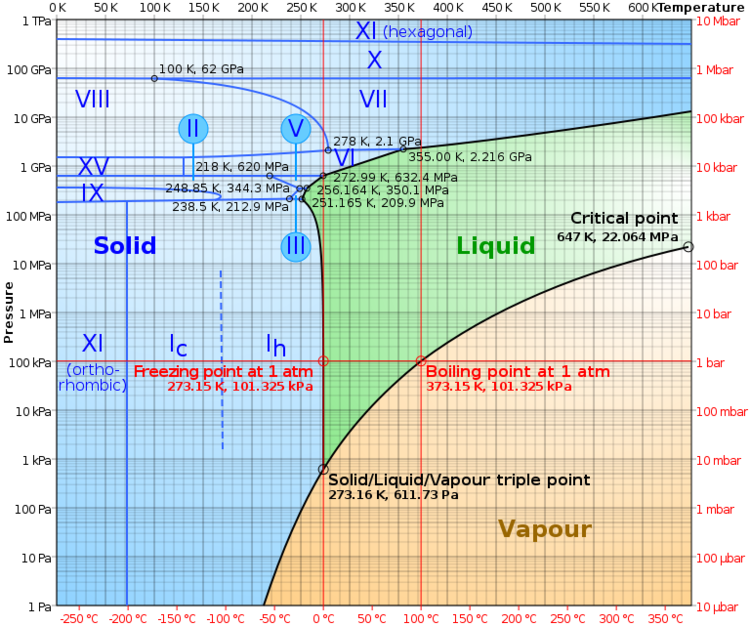
  • UPDATE(2/29/12): I'm very optimistic now that the refrigeration coils from a standard chest freezer should be sufficient for this task. The information I'm finding on the web indicates that the coils themselves can easily achieve temperatures around -25°C (~248°K) under normal operation. If you look at the phase diagram above you'll see that at -25°C water would be solid phase at any pressure above about 60 Pascal. This gives the system a pretty decent operating range for pressures (~60Pa - 611.73Pa) without requiring any specialized cryogenic equipment.
    • Below about 60 Pascal the water vapor in the chamber would not be able to collect and freeze on the -25°C coils. It would instead just accumulate as vapor in the chamber, raising the pressure until it was high enough for water molecules to freeze as ice on the coils. This freezing would in turn lower the pressure, meaning that there should be a stable equilibrium pressure of ~60Pa ideally. That's an ideal scenario that assumes that there's nothing in the chamber but water vapor. In practice the equilibrium pressure will probably be a skooch higher.
    • Above 611.73Pa ice will no longer sublimate, but will start going through the water phase again.


  • UPDATE(11/15/12): I'm still fairly confident that refrigeration coils will, in principle, do the job. It does, however, seem like their use may be a bit too complicated, at least for a first time, low budget, small scale build. I've recently been tipped off by someone that silica desiccant crystals may provide a much easier alternative. Putting a tray of silica crystals in the bottom of the vacuum chamber would be much cheaper and simpler than trying to run the tubes for a set of refrigeration coils into and out of the vacuum chamber (and pressure sealing those holes). Also, once the silica crystals have absorbed their limit of moisture, they can simply be baked in the oven to remove that moisture, allowing for constant reuse. The only problem I foresee is that I do not know how they behave in low pressure environments and if at that pressure they will still be able to absorb moisture, and do so at a sufficient rate to maintain the vacuum. I'll need do some research to verify that they will work for this application, but for the moment it seems very promising. Also, I plan on going ahead and ordering some silica crystals so I can do some hands on experiments.
    • Apparently "Fresh Step Crystal Kitty Litter" is supposed to be 100% silica gel, so I'm thinking this will be a nice cheap, low grade source for early experiments.
    • UPDATE(05/12/14) Initial tests of this method do not seem promising, at least not for the vacuum freeze drying method. I will, of course, still want to run a few more experiments to be sure of this, but it seems that the low pressure inhibits the silica gel's ability to absorb the water vapor.
      • Note: This method may still prove viable for more normal pressure "frostless freezer" drying.
  • UPDATE(06/04/14):Talked with a retired HVAC engineer for quite a while yesterday. Very informative, I feel like I have a significantly better grasp about how these systems function now. I am bolstered in my confidence that I can make this approach work, provided I have enough cleverness in me.
    • Also found some very useful and promising information today.
      • QUOTE: The lowest temperature that can practically be achieved in single-stage refrigeration systems is about -40ºF to -50ºF [-58 to -40ºC]. A single-stage system is limited by the compression ratio of the compressor and the ambient temperature in which it must condense the refrigerant. Temperatures from -50ºF down to -120ºF or lower can only be achieved economically by using cascade refrigeration systems. SOURCE: 2011 Refrigerant Reference Guide, P.64.
    • Now I just have to figure how to make that kind of system on the cheap.


Ideas

Sublimative Boost Cooling

  • I have heard somewhere (I think it may have been one of Applied Science's videos on youtube) that to properly freeze dry things containing large amounts of sucrose (like ice cream) you have to cool it down into the -30 to -35ºC range.
  • I believe it may be nonessential, as it may only affect the final texture and not the actual preservation.
  • I believe I can still achieve this without dry ice, however.
    • As ice sublimates off under low pressure, it cools the material, much in the same way evaporative cooling works.
    • This effect could/should be sufficient to boost a -20ºC sample down farther, into the necessary range
    • Have a cooling cycle at the beginning of the process.
      • Driven by the vacuum pump instead of the cryo deposition coils, allowing it to hit temperatures below those the cryo coils can generate


Cascade Cryo Cooling

  • If the temperatures achieved by an unmodified refrigeration system from a freezer proves insufficient to make the system work, it should be possible to get even lower temperatures by cascading two inexpensive systems
    • Use two compressor based systems in series; the cooling tubes of the secondary interfaced with the heat disipator of the primary(which then cools the deposition coils). This gives the system as a whole a greater ΔT
    • Peltier cooler chained with a compressor cooler might also be a method


Resources

Research

Basics of Vacuum Technology
Using Vacuum Freeze-Drying to Salvage Water-Damaged Archival Materials
HowStuffWorks.com: Freeze Drying
Introduction to Vacuum Gauges and other vacuum technology

The Vacuum Lab: A Journal of Practical and Useful Vacuum Technology
Pumping Water Vapor

Robinar A/C: Fundamentals of Dehydrating a Refrigerant System

About.com Inventor: Freeze Drying & Freeze Dried Food

Building a Freeze Dryer; Forum Discussion at Refrigeration-Engineer.com Posts# 15 and 2 are especially useful
Building a Freeze Dryer: Revisited; Forum Discussion at Refrigeration-Engineer.com
Peltier Cooler: info page on heatsink-guide.com


Polycold PFC Cryopumps Page 2 Has a useful table
[1]


Refrigerants

2011 Refrigerant Reference Guide Super Useful: P.64
ALTERNATIVE WORKING FLUIDS PERFORMANCE

Robinar A/C: Fundamentals of Dehydrating a Refrigerant System

Silica Gela and Desiccants:

Wikipedia: Adsorption
[2]
[3]
[4]
[5]
Desiccant Types

Current Commercial Products:

http://harvestright.com/in-home-freeze-dryer/


Retrieved from "https://256.makerslocal.org/wiki/index.php?title=DIY_Freeze_Dryer&oldid=18031"